Уравнения касательной и нормали к поверхности. Касательная плоскость к поверхности второго порядка

Графиком функции 2-х переменных z = f(x,y) является поверхность, проектирующаяся на плоскость XOY в область определения функции D.
Рассмотрим поверхность σ , заданную уравнением z = f(x,y) , где f(x,y) – дифференцируемая функция, и пусть M 0 (x 0 ,y 0 ,z 0) – фиксированная точка на поверхности σ , т.е. z 0 = f(x 0 ,y 0). Назначение . Онлайн-калькулятор предназначен для нахождения уравнения касательной плоскости и нормали к поверхности . Решение оформляется в формате Word . Если необходимо найти уравнение касательной к кривой (y = f(x)), то необходимо использовать данный сервис .

Правила ввода функций :

Правила ввода функций :

1. Все переменные выражаются через x,y,z

Касательной плоскостью к поверхности σ в её точке М 0 называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М 0 .
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M 0 (x 0 ,y 0 ,z 0) имеет вид:

z – z 0 = f’ x (x 0 ,y 0)(x – x 0) + f’ y (x 0 ,y 0)(y – y 0)

Вектор называется вектором нормали к поверхности σ в точке М 0 . Вектор нормали перпендикулярен касательной плоскости.
Нормалью к поверхности σ в точке М 0 называется прямая, проходящая через эту точку и имеющая направление вектора N.
Канонические уравнения нормали к поверхности, заданной уравнением z = f(x,y) , в точке M 0 (x 0 ,y 0 ,z 0), где z 0 = f(x 0 ,y 0), имеют вид:

Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M 0 (0;1).
Решение . Запишем уравнения касательной в общем виде: z - z 0 = f" x (x 0 ,y 0 ,z 0)(x - x 0) + f" y (x 0 ,y 0 ,z 0)(y - y 0)
По условию задачи x 0 = 0 , y 0 = 1 , тогда z 0 = 5
Найдем частные производные функции z = x^3+5*y:
f" x (x,y) = (x 3 +5 y)" x = 3 x 2
f" x (x,y) = (x 3 +5 y)" y = 5
В точке М 0 (0,1) значения частных производных:
f" x (0;1) = 0
f" y (0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М 0: z - 5 = 0(x - 0) + 5(y - 1) или -5 y+z = 0

Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M 0 (1;0;1).
Решение . Находим частные производные функции . Поскольку функция задана в неявном виде, то производные ищем по формуле:

Для нашей функции:

Тогда:

В точке М 0 (1,0,1) значения частных производных:
f" x (1;0;1) = -3 / 16
f" y (1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М 0: z - 1 = -3 / 16 (x - 1) + 0(y - 0) или 3 / 16 x+z- 19 / 16 = 0

Пример . Поверхность σ задана уравнением z = y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М 0 (x 0 , y 0 , z 0), принадлежащей ей, если x 0 = –1, y 0 = 2.
Найдем частные производные функции z = f (x , y ) = y/x + xy – 5x 3:
f x ’(x , y ) = (y/x + xy – 5x 3)’ x = – y/x 2 + y – 15x 2 ;
f y ’ (x , y ) = (y/x + xy – 5x 3)’ y = 1/x + x .
Точка М 0 (x 0 , y 0 , z 0) принадлежит поверхности σ , поэтому можно вычислить z 0 , подставив заданные x 0 = –1 и y 0 = 2 в уравнение поверхности:

z = y/x + xy – 5x 3

z 0 = 2/(-1) + (–1) 2 – 5 (–1) 3 = 1.
В точке М 0 (–1, 2, 1) значения частных производных:
f x ’(М 0) = –1/(-1) 2 + 2 – 15(–1) 2 = –15; f y ’(М 0) = 1/(-1) – 1 = –2.
Пользуясь формулой (5) получаем уравнение касательной плоскости к поверхности σ в точке М 0:
z – 1= –15(x + 1) – 2(y – 2) z – 1= –15x – 15 – 2y + 4 15x + 2y + z + 10 = 0.
Пользуясь формулой (6) получаем канонические уравнения нормали к поверхности σ в точке М 0: .
Ответы: уравнение касательной плоскости: 15x + 2y + z + 10 = 0; уравнения нормали: .

Пример №1 . Дана функция z=f(x,y) и две точки А(х 0 , y 0) и В(х 1 ,y 1). Требуется: 1) вычислить значение z 1 функции в точке В; 2) вычислить приближенное значение z 1 функции в точке В исходя из значения z 0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x 0 ,y 0 ,z 0).
Решение.
Запишем уравнения касательной в общем виде:
z - z 0 = f" x (x 0 ,y 0 ,z 0)(x - x 0) + f" y (x 0 ,y 0 ,z 0)(y - y 0)
По условию задачи x 0 = 1, y 0 = 2, тогда z 0 = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f" x (x,y) = (x 2 +3 x y +y 2)" x = 2 x+3 y 3
f" x (x,y) = (x 2 +3 x y +y 2)" y = 9 x y 2
В точке М 0 (1,2) значения частных производных:
f" x (1;2) = 26
f" y (1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М 0:
z - 25 = 26(x - 1) + 36(y - 2)
или
-26 x-36 y+z+73 = 0

Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).

Поверхность определяется как множество точек , координаты которых удовлетворяют определённому виду уравнений:

F (x , y , z) = 0 (1) {\displaystyle F(x,\,y,\,z)=0\qquad (1)}

Если функция F (x , y , z) {\displaystyle F(x,\,y,\,z)} непрерывна в некоторой точке и имеет в ней непрерывные частные производные, по крайней мере одна из которых не обращается в нуль, то в окрестности этой точки поверхность, заданная уравнением (1), будет правильной поверхностью .

Помимо указанного выше неявного способа задания , поверхность может быть определена явно , если одну из переменных, например, z, можно выразить через остальные:

z = f (x , y) (1 ′) {\displaystyle z=f(x,y)\qquad (1")}

Более строго, простой поверхностью называется образ гомеоморфного отображения (то есть взаимно однозначного и взаимно непрерывного отображения) внутренности единичного квадрата. Этому определению можно дать аналитическое выражение.

Пусть на плоскости с прямоугольной системой координат u и v задан квадрат , координаты внутренних точек которого удовлетворяют неравенствам 0 < u < 1, 0 < v < 1. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул х = x(u, v), у = y(u, v), z = z(u, v) (параметрическое задание поверхности). При этом от функций x(u, v), y(u, v) и z(u, v) требуется, чтобы они были непрерывными и чтобы для различных точек (u, v) и (u", v") были различными соответствующие точки (x, у, z) и (x", у", z").

Примером простой поверхности является полусфера. Вся же сфера не является простой поверхностью . Это вызывает необходимость дальнейшего обобщения понятия поверхности.

Подмножество пространства, у каждой точки которого есть окрестность, являющаяся простой поверхностью , называется правильной поверхностью .

Поверхность в дифференциальной геометрии

Геликоид

Катеноид

Метрика не определяет однозначно форму поверхности. Например, метрики геликоида и катеноида , параметризованных соответствующим образом, совпадают, то есть между их областями существует соответствие, сохраняющее все длины (изометрия). Свойства, сохраняющиеся при изометрических преобразованиях, называются внутренней геометрией поверхности. Внутренняя геометрия не зависит от положения поверхности в пространстве и не меняется при её изгибании без растяжения и сжатия (например, при изгибании цилиндра в конус) .

Метрические коэффициенты E , F , G {\displaystyle E,\ F,\ G} определяют не только длины всех кривых, но и вообще результаты всех измерений внутри поверхности (углы, площади, кривизна и др.). Поэтому всё, что зависит только от метрики, относится к внутренней геометрии.

Нормаль и нормальное сечение

Векторы нормали в точках поверхности

Одной из основных характеристик поверхности является её нормаль - единичный вектор, перпендикулярный касательной плоскости в заданной точке:

m = [ r u ′ , r v ′ ] | [ r u ′ , r v ′ ] | {\displaystyle \mathbf {m} ={\frac {[\mathbf {r"_{u}} ,\mathbf {r"_{v}} ]}{|[\mathbf {r"_{u}} ,\mathbf {r"_{v}} ]|}}} .

Знак нормали зависит от выбора координат.

Сечение поверхности плоскостью, содержащей нормаль поверхности в заданной точке, образует некоторую кривую, которая называется нормальным сечением поверхности. Главная нормаль для нормального сечения совпадает с нормалью к поверхности (с точностью до знака).

Если же кривая на поверхности не является нормальным сечением, то её главная нормаль образует с нормалью поверхности некоторый угол θ {\displaystyle \theta } . Тогда кривизна k {\displaystyle k} кривой связана с кривизной k n {\displaystyle k_{n}} нормального сечения (с той же касательной) формулой Мёнье :

k n = ± k cos θ {\displaystyle k_{n}=\pm k\,\cos \,\theta }

Координаты орта нормали для разных способов задания поверхности приведены в таблице:

	Координаты нормали в точке поверхности
неявное задание	(∂ F ∂ x ; ∂ F ∂ y ; ∂ F ∂ z) (∂ F ∂ x) 2 + (∂ F ∂ y) 2 + (∂ F ∂ z) 2 {\displaystyle {\frac {\left({\frac {\partial F}{\partial x}};\,{\frac {\partial F}{\partial y}};\,{\frac {\partial F}{\partial z}}\right)}{\sqrt {\left({\frac {\partial F}{\partial x}}\right)^{2}+\left({\frac {\partial F}{\partial y}}\right)^{2}+\left({\frac {\partial F}{\partial z}}\right)^{2}}}}}
явное задание	(− ∂ f ∂ x ; − ∂ f ∂ y ; 1) (∂ f ∂ x) 2 + (∂ f ∂ y) 2 + 1 {\displaystyle {\frac {\left(-{\frac {\partial f}{\partial x}};\,-{\frac {\partial f}{\partial y}};\,1\right)}{\sqrt {\left({\frac {\partial f}{\partial x}}\right)^{2}+\left({\frac {\partial f}{\partial y}}\right)^{2}+1}}}}
параметрическое задание	(D (y , z) D (u , v) ; D (z , x) D (u , v) ; D (x , y) D (u , v)) (D (y , z) D (u , v)) 2 + (D (z , x) D (u , v)) 2 + (D (x , y) D (u , v)) 2 {\displaystyle {\frac {\left({\frac {D(y,z)}{D(u,v)}};\,{\frac {D(z,x)}{D(u,v)}};\,{\frac {D(x,y)}{D(u,v)}}\right)}{\sqrt {\left({\frac {D(y,z)}{D(u,v)}}\right)^{2}+\left({\frac {D(z,x)}{D(u,v)}}\right)^{2}+\left({\frac {D(x,y)}{D(u,v)}}\right)^{2}}}}}

Здесь D (y , z) D (u , v) = | y u ′ y v ′ z u ′ z v ′ | , D (z , x) D (u , v) = | z u ′ z v ′ x u ′ x v ′ | , D (x , y) D (u , v) = | x u ′ x v ′ y u ′ y v ′ | {\displaystyle {\frac {D(y,z)}{D(u,v)}}={\begin{vmatrix}y"_{u}&y"_{v}\\z"_{u}&z"_{v}\end{vmatrix}},\quad {\frac {D(z,x)}{D(u,v)}}={\begin{vmatrix}z"_{u}&z"_{v}\\x"_{u}&x"_{v}\end{vmatrix}},\quad {\frac {D(x,y)}{D(u,v)}}={\begin{vmatrix}x"_{u}&x"_{v}\\y"_{u}&y"_{v}\end{vmatrix}}} .

Все производные берутся в точке (x 0 , y 0 , z 0) {\displaystyle (x_{0},y_{0},z_{0})} .

Кривизна

Для разных направлений в заданной точке поверхности получается разная кривизна нормального сечения, которая называется нормальной кривизной ; ей приписывается знак плюс, если главная нормаль кривой идёт в том же направлении, что и нормаль к поверхности, или минус, если направления нормалей противоположны.

Вообще говоря, в каждой точке поверхности существуют два перпендикулярных направления e 1 {\displaystyle e_{1}} и e 2 {\displaystyle e_{2}} , в которых нормальная кривизна принимает минимальное и максимальное значения; эти направления называются главными . Исключение составляет случай, когда нормальная кривизна по всем направлениям одинакова (например, у сферы или на торце эллипсоида вращения), тогда все направления в точке - главные.

Поверхности с отрицательной (слева), нулевой (в центре) и положительной (справа) кривизной.

Нормальные кривизны в главных направлениях называются главными кривизнами ; обозначим их κ 1 {\displaystyle \kappa _{1}} и κ 2 {\displaystyle \kappa _{2}} . Величина:

K = κ 1 κ 2 {\displaystyle K=\kappa _{1}\kappa _{2}}

Определение. Точка , лежащая на поверхности второго порядка, заданной относительно ОДСК общим уравнением (1) называется неособой, если среди трёх чисел: есть хотя бы одно, не равное нулю.

Таким образом, точка , лежащая на поверхности второго порядка, является не особой тогда и только тогда, когда она является её центром, иначе, когда поверхность коническая, а точка - вершина этой поверхности.

Определение. Касательной прямой к поверхности второго порядка в данной на ней не особой точке называется прямая, проходящая через эту точку, пересекающая поверхность второго порядка в дву-кратной точке или являющаяся прямолинейной образующей поверхности.

Теорема 3. Касательные прямые к поверхности второго порядка в данной на ней не особой точке лежат в одной плоскости, называемой касательной плоскостью к поверхности в рассматриваемой точке. Уравнение касательной плоскости имеет

Доказательство. Пусть , , параметрические уравнения прямой, проходящей через неособую точку по-верхности второго порядка, заданной уравнением (1). Подставляя в уравнение (1) , , вместо , , , получим:

Так как точка лежит на поверхности (1), то и из уравнения (3) находим (это значение соответствует точке ). Для того, чтобы точка пересечения прямой с поверхностью (1) была двойной, или чтобы прямая целиком лежала на поверхности, необходимо и достаточно, чтобы выполнялось равенство:

Если при этом:

То точка пересечения прямой линии с поверхностью (1) двойная. А если:

То прямая целиком лежит на поверхности (1).

Из соотношений (4) и , , следует, что координаты , , любой точки , лежащей на любой касательной к поверхности (1) удовлетворяют уравнению:

Обратно, если координаты какой-нибудь точки , отличной от , удовлетворяют этому уравнению, то координаты , , вектора , удовлетворяют соотношению (4), а это значит, что прямая - касательная к рассматриваемой поверхности.

Так как точка - неособая точка поверхности (1), то среди чисел , , есть по крайней мере одно, не равное нулю; значит уравнение (5) есть уравнение первой степени относительно . Это и есть уравнение плоскости, касательной к поверхности (1) в данной на ней не особой точке .

Исходя из канонических уравнений поверхностей второго порядка легко составить уравнения касательных плоскостей к эллипсоиду, гиперболоиду и т.д. в данной на них точке .

1). Касательная плоскость к эллипсоиду:

2). Касательная плоскость к одно и двуполостному гиперболоидам:

3). Касательная плоскость к эллиптическому и гиперболическому параболоидам:

§ 161.Пересечение касательной плоскости с поверхностью второго порядка.

Примем неособую точку поверхности второго порядка за начало координат ОДСК, оси и расположим в плоскости касательной к поверхности в точке . Тогда в общем уравнении поверхности (1) свободный член равен нулю: , а уравнение плос-кости, касающейся поверхности в начале координат, должно иметь вид: .

Но уравнение плоскости, проходящей через начало координат имеет вид: .

И, так как это уравнение должно быть эквивалентно уравнению , то , , .

Итак, в выбранной системе координат уравнение поверхности (1) должно иметь вид:

Обратно, если , то уравнение (6) является уравнением поверхности, проходящей через начало координат , а плоскость - касательная плоскость к этой поверхности в точке . Уравнение линии, по которой касательная плоскость к поверхности в точке пересекает поверхность (6) имеет вид:

Если . Это инвариант в теории инвариантов для линий второго порядка. Уравнение (7)

Это же линия второго порядка. По виду этой линии инвариант , поэтому:

При здесь две мнимые пересекающиеся прямые.

При - две действительные пересекающиеся прямые.

Если , но хотя бы один из коэффициентов , , не равен нулю, то линия пересечения (7) - две совпадающие прямые.

Наконец, если , то плоскость

входит в состав данной поверхности, а сама поверхность распадается, следовательно, на пару плоскостей

§ 162.Эллиптические, гиперболические или параболические точки поверхности второго порядка.

1. Пусть касательная плоскость к поверхности второго порядка в точке пересекает её по двум мни-мым пересекающимся прямым. В этом случае точка называется эллиптической точкой поверхности.

2. Пусть касательная плоскость к поверхности второго порядка в точке пересекает её по двум действительным прямым, пересекающимся в точке касания. В этом случае точка называется гиперболической точкой поверхности.

3. Пусть касательная плоскость к поверхности второго порядка в точке пересекает её по двум совпадающим прямым. В этом случае точка называется параболической точкой поверхности.

Теорема 4. Пусть поверхность второго порядка относительно ОДСК задана уравнением (1) и данное уравнение (1) является уравнением действительной нераспадающейся поверхностью второго порядка. Тогда, если ; то все точки поверхности эллиптические.

Доказательство. Введём новую систему координат , выбирая за начало координат любую неособую точку данной поверхности и располагая оси и в плоскости, касательной к поверхности в точке . Уравнение (1) в новой системе координат преобразуется к виду:

Где . Вычислим инвариант для этого уравнения .

Так как при переходе от одной ОДСК к другой ОДСК знак не меняется, то знаки и противоположны, поэтому, если , то ; и, как следует из классификации (см. § 161) касательная плоскость к поверхности в точке пересекает поверхность по двум мнимым пересекающимся прямым, т.е. - эллиптическая точка.

2) Однополостный гиперболоид и гиперболический параболоид состоят из гиперболических точек.

3) Действительный конус второго порядка (вершина исключается), эллиптический (действительный), гиперболический и параболический цилиндры состоят из параболических точек.

Параболический цилиндр .

Чтобы определить расположение параболического цилиндра, достаточно знать:

1) плоскость симметрии, параллельную образующим цилиндра;

2) касательную плоскость к цилиндру, перпендикулярную к этой плоскости симметрии;

3) вектор, перпендикулярный к этой касательной плоскости и направленный в сторону вогнутости цилиндра.

В случае, если общее уравнение определяет параболический цилиндр, оно может быть переписано в виде:

Подберем m так, чтобы плоскости

были бы взаимно перпендикулярными:

При этом значении m плоскость

будет плоскостью симметрии, параллельной образующим цилиндра.

Плоскость

будет касательной плоскостью к цилиндру, перпендикулярной к указанной плоскости симметрии, а вектор

будет перпендикулярен к найденной касательной плоскости и направлен в сторону вогнутости цилиндра.

Скачать с Depositfiles

4. ТЕОРИЯ ПОВЕРХНОСТЕЙ.

4.1 УРАВНЕНИЯ ПОВЕРХНОСТЕЙ.

Поверхность в трёхмерном пространстве может быть задана:

1) неявно: F ( x , y , z ) =0 (4.1)

2) явно: z = f ( x , y ) (4.2)

3) параметрически: (4.3)

или:
(4.3’)

где скалярные аргументы
иногда называют криволинейными координатами. Например, сферу
удобно задавать в сферических координатах:
.

4.2 КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К ПОВЕРХНОСТИ.

Если линия лежит на поверхности (4.1), то координаты её точек удовлетворяют уравнению поверхности:

Дифференцируя это тождество, получим:

(4.4)

или
(4.4 ’ )

в каждой точке кривой на поверхности. Таким образом, вектор градиента в неособых точках поверхности (в которых функция (4.5) дифференцируема и
) перпендикулярен касательным векторам к любым линиям на поверхности, т.е может быть использован в качестве вектора нормали для составления уравнения касательной плоскости в точке М 0 (x 0 , y 0 , z 0 ) поверхности

(4.6)

и в качестве направляющего вектора в уравнении нормали:

(4.7)

В случае явного (4.2) задания поверхности уравнения касательной плоскости и нормали соответственно примут вид:

(4.8)

и
(4.9)

При параметрическом представлении поверхности (4.3) векторы
лежат в касательной плоскости и уравнение касательной плоскости может быть записано в виде:

(4.10)

а в качестве направляющего вектора нормали может быть принято их векторное произведение:

и уравнение нормали может быть записано в виде:

(4.11)

где
— значения параметров соответствующие точке М 0 .

В дальнейшем мы ограничимся рассмотрением лишь таких точек поверхности, где векторы

не равны нулю и не параллельны.

Пример 4.1 Составить уравнения касательной плоскости и нормали в точке М 0 (1,1,2) к поверхности параболоида вращения
.

Решение: Так как уравнение параболоида задано в явном виде, то согласно (4.8) и (4.9) нужно найти
в точке М 0 :

, а в точке М 0
. Тогда уравнение касательной плоскости в точке М 0 примет вид:

2(x -1)+2(y -1)-(z -2)=0 или 2 x +2 y – z ‑ 2=0, а уравнение нормали
.

Пример 4.2 Составить уравнения касательной плоскости и нормали в произвольной точке геликоида
, .

Решение. Здесь ,

Уравнение касательной плоскости:

или

Уравнения нормали:

.

4.3 ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ.

Если поверхность задается уравнением

то кривая
на ней может быть задана уравнением
(4.12)

Дифференциал радиус-вектора
вдоль кривой, отвечающий смещению из точки М 0 в близлежащую точку М, равен

(4.13)

Так как
— дифференциал дуги кривой, отвечающий тому же смещению), то

(4.14)

где .

Выражение в правой части (4.14) называется первой квадратичной формой поверхности и играет в теории поверхностей огромную роль.

Интегрирую дифференциал ds в пределах от t 0 (соответствует точке М 0 ) до t (соответствует точке М), получим длину соответствующего отрезка кривой

(4.15)

Зная первую квадратичную форму поверхности, можно находить не только длины, но и углы между кривыми.

Если du , dv — дифференциалы криволинейных координат, отвечающие бесконечно малому смещению по одной кривой, а
— по другой, то с учетом (4.13):

(4.16)

С помощью формулы

(4.17)

первая квадратичная форма дает возможность вычислить площадь области
поверхности.

Пример 4.3 На геликоиде , найти длину винтовой линии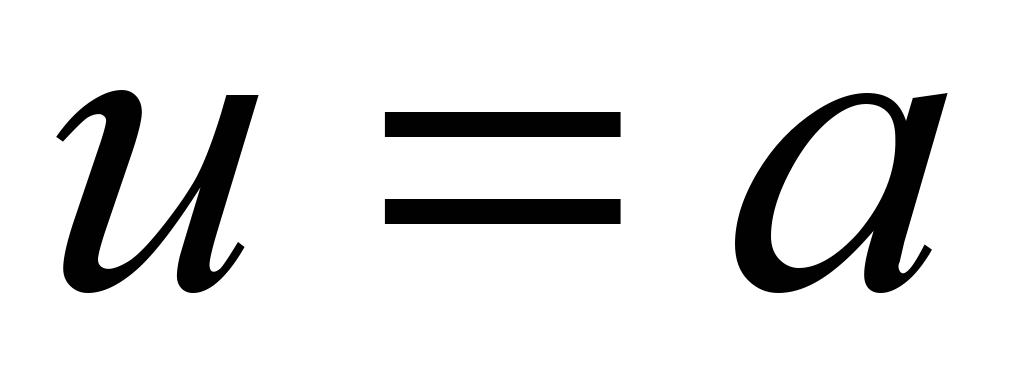
между двумя точками .

Решение. Поскольку на винтовой линии
, то . Найдём в точке
первую квадратичную форму. Обозначив и v = t , получим уравнение данной винтовой линии в виде . Квадратичная форма:

= ‑ первая квадратичная форма.

Здесь . В формуле (4.15) в данном случае
и длина дуги:

=

4.4 ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ.

Обозначим
‑ единичный вектор нормали к поверхности
:

(4.18) . (4.23)

Линия на поверхности называется линией кривизны, если ее направление в каждой точке является главным направлением.

4.6 ПОНЯТИЕ О ГЕОДЕЗИЧЕСКИХ ЛИНИЯХ НА ПОВЕРХНОСТИ.

Определение 4.1 . Кривая на поверхности называется геодезической, если ее главная нормаль в каждой точке, где кривизна отлична от нуля, совпадает с нормалью к поверхности.

Через каждую точку поверхности в любом направлении проходит, и при том только одна геодезическая. На сфере, например, геодезическими являются большие круги.

Параметризация поверхности называется полугеодезической, если одно семейство координатных линий состоит из геодезических, а второе ему ортогонально. Например, на сфере меридианы (геодезические) и параллели.

Геодезическая на достаточно малом отрезке является кратчайшей среди всех близких к ней кривых, соединяющих те же точки.

Пусть имеем поверхность, заданную уравнением вида

Введем следующее определение.

Определение 1. Прямая линия называется касательной к поверхности в некоторой точке , если она является

касательной к какой-либо кривой, лежащей на поверхности и проходящей через точку .

Так как через точку Р проходит бесконечное число различных кривых, лежащих на поверхности, то и касательных к поверхности, проходящих через эту точку, будет, вообще говоря, бесконечное множество.

Введем понятие об особых и обыкновенных точках поверхности

Если в точке все три производные равны нулю или хотя бы одна из этих производных не существует, то точка М называется особой точкой поверхности. Если в точке все три производные существуют и непрерывны, причем хотя бы одна из них отлична от нуля, то точка М называется обыкновенной точкой поверхности.

Теперь мы можем сформулировать следующую теорему.

Теорема. Все касательные прямые к данной поверхности (1) в ее обыкновенной точке Р лежат в одной плоскости.

Доказательство. Рассмотрим на поверхности некоторую линию L (рис. 206), проходящую через данную точку Р поверхности. Пусть рассматриваемая кривая задана параметрическими уравнениями

Касательная к кривой будет касательной к поверхности. Уравнения этой касательной имеют вид

Если выражения (2) подставить в уравнение (1), то это уравнение превратится в тождество относительно t, так как кривая (2) лежит на поверхности (1). Дифференцируя его по получим

Проекции этого вектора зависят от - координат точки Р; заметим, что так как точка Р обыкновенная, то эти проекции в точке Р одновременно не обращаются в нуль и потому

касательный к кривой, проходящей через точку Р и лежащей на поверхности. Проекции этого вектора вычисляются на основании уравнений (2) при значении параметра t, соответствующем точке Р.

Вычислим скалярное произведение векторов N и которое равно сумме произведений одноименных проекций:

На основании равенства (3) выражение, стоящее в правой части, равно нулю, следовательно,

Из последнего равенства следует, что вектор ЛГ и касательный вектор к кривой (2) в точке Р перпендикулярны. Проведенное рассуждение справедливо для любой кривой (2), проходящей через точку Р и лежащей на поверхности. Следовательно, каждая касательная к поверхности в точке Р перпендикулярна к одному и тому же вектору N и потому все эти касательные лежат в одной плоскости, перпендикулярной к вектору ЛГ. Теорема доказана.

Определение 2. Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную ее точку Р, называется касательной плоскостью к поверхности в точке Р (рис. 207).

Заметим, что в особых точках поверхности может не существовать касательной плоскости. В таких точках касательные прямые к поверхности могут не лежать в одной плоскости. Так, например, вершина конической поверхности является особой точкой.

Касательные к конической поверхности в этой точке не лежат в одной плоскости (они сами образуют коническую поверхность).

Напишем уравнение касательной плоскости к поверхности (1) в обыкновенной точке. Так как эта плоскость перпендикулярна вектору (4), то, следовательно, ее уравнение имеет вид

Если уравнение поверхности задано в форме или уравнение касательной плоскости в этом случае примет вид

Замечание. Если в формуле (6) положим , то эта формула примет вид

ее правая часть представляет собой полный дифференциал функции . Следовательно, . Таким образом, полный дифференциал функции двух переменных в точке соответствующий приращениям независимых переменных х и у, равен соответствующему приращению аппликаты касательной плоскости к поверхности, которая является графиком данной функции.

О пределение 3. Прямая, проведенная через точку поверхности (1) перпендикулярно к касательной плоскости, называется нормалью к поверхности (рис. 207).

Напишем уравнения нормали. Так как ее направление совпадает с направлением вектора N, то ее уравнения будут иметь вид