Метод неизвестных коэффициентов. Интегрирование дробно-рациональной функции

МИНИСТЕРСТВО НАУКИ И ОБРАЗОВАНИЯ РЕСПУБЛИКИ БАШКОРТО СТАН

ГАОУ СПО Башкирский архитектурно-строительный колледж

Халиуллин Асхат Адельзянович,

преподаватель математики Башкирского

архитектурно-строительного колледжа

г.УФА

2014 г.

Введение ___________________________________________________3

Глава I . Теоретические аспекты использования метода неопределенных коэффициентов______________________________________________4

Глава II . Поиски решения задач с многочленами методом неопределенныхкоэффициентов_______________________________7

2.1.Разложение многочлена на множители_____________________ 7

2.2. Задачи с параметрами__________________________________ 10

2.3. Решение уравнений____________________________________14

2.4. Функциональные уравнения_____________________________19

Заключение_________________________________________________23

Список использованной литературы____________________________24

Приложение________________________________________________25

Введение.

Данная работа посвящена теоретическим и практическим аспектам внедрения в школьный курс математики метода неопределенных коэффициентов. Актуальность данной темы определяется следующими обстоятельствами.

Никто не будет спорить с тем, что математика как наука не стоит на одном месте, все время развивается, появляются новые задачи повышенной сложности, что часто вызывает определенные трудности, поскольку эти задачи, как правило, связаны с исследованием. Такие задачи в последние годы предлагались на школьных, районных и республиканских математических олимпиадах, они также имеются в вариантах ЕГЭ. Поэтому потребовалось специальный метод, который позволял бы наиболее быстро, эффективно и доступно решать хотя бы часть из них. В этой работе доступно излагается содержание метода неопределенных коэффициентов, широко применяющегося в самых разнообразных разделах математики, начиная от вопросов, входящих в курс общеобразовательной школы, и до самых продвинутых ее частей. В частности, применения метода неопределенных коэффициентов в решении задач с параметрами, дробно-рациональных и функциональных уравнений особенно интересны и эффективны; они легко могут заинтересовать любого, кто интересуется математикой. Главная цель предлагаемой работы и подборки задач состоит в том, чтобы предоставить широкие возможности для оттачивания и развития способности находить короткие и нестандартные решения.

Данная работа состоит из двух глав. В первой рассматриваются теоретические аспекты использования

метода неопределенных коэффициентов, во второй-практико-методологические аспекты такого использования.

В приложении к работе приведены условия конкретных задач для самостоятельного решения.

Глава I . Теоретические аспекты использования метода неопределенных коэффициентов

«Человек … родился быть господином,

повелителем, царем природы, но мудрость,

с которой он должен править, не дана ему

от рождения: она приобретается учением»

Н.И.Лобачевский

Существуют различные способы и методы решения задач, но одним из самым удобным, наиболее эффективным, оригинальным, изящным и вместе с тем очень простым и понятным всем является метод неопределенных коэффициентов. Метод неопределенных коэффициентов -метод, применяемый в математике для отыскания коэффициентов выражений, вид которых заранее известен.

Прежде чем рассмотреть применение метода неопределенных коэффициентов к решению различного рода задач, приведем ряд сведений теоретического характера.

Пусть даны,

A n (x ) = a 0 x n + a 1 x n-1 + a 2 x n-2 + ··· + a n-1 x + a n

B m (x ) = b 0 x m + b 1 x m -1 + b 2 x m -2 + ··· + b m-1 x + b m ,

многочлены относительно х с любыми коэффициентами.

Теорема. Два многочлена, зависящие от одного и того же аргумента,тождественно равны в том и только в том случае, если n = m и их соответственные коэффициенты равны a 0 = b 0 , a 1 = b 1 , a 2 = b 2 ,··· , a n -1 = b m -1 , a n = b m и т . д .

Очевидно, что равные многочлены принимают при всех значениях х одинаковые значения. И наоборот, если значения двух многочленов равны при всех значениях х , то многочлены равны, то есть их коэффициенты при одинаковых степенях х совпадают.

Следовательно, идея применения метода неопределенных коэффициентов к решению задач состоит в следующем.

Пусть нам известно, что в результате некоторых преобразований получается выражение определенного вида и неизвестны лишь коэффициенты в этом выражении. Тогда эти коэффициенты обозначают буквами и рассматривают как неизвестные. Затем для определения этих неизвестных составляется система уравнений.

Например, в случае многочленов эти уравнения составляют из условия равенства коэффициентов при одинаковых степенях х у двух равных многочленов.

Покажем сказанное выше на следующих конкретных примерах, причем начнем с самого простого.

Так, например, на основании теоретических соображений дробь

может быть представлена в виде суммы

, где a , b и c - коэффициенты, подлежащие определению. Чтобы найти их, приравниваем второе выражение первому:

=

и освобождаясь от знаменателя и собирая слева члены с одинаковыми степенями х , получаем:

(a + b + c )х 2 + ( b - c )х - а = 2х 2 – 5 х – 1

Так как последнее равенство должно выполняться для всех значений х , то коэффициенты при одинаковых степенях х справа и слева должны быть одинаковы. Таким образом, получаются три уравнения для определения трех неизвестных коэффициентов:

a + b + c = 2

b - c = - 5

а = 1 , откуда a = 1 , b = - 2 , c = 3

Следовательно,

=
,

справедливость этого равенства легко проверить непосред-ственно.

Пусть ещё нужно представить дробь

в виде a + b
+ c
+ d
, где a , b , c и d - неизвестные рациональные коэффициенты. Приравниваем второе выражение первому:

a + b
+ c
+ d
=
или, освобождаясь от знаменателя, вынося, где можно, рациональные множители из-под знаков корней и приводя подобные члены в левой части, получаем:

(a - 2 b + 3 c ) + (- a + b +3 d )
+ (a + c - 2 d )
+

+ (b - c + d )
= 1 +
-
.

Но такое равенство возможно лишь в случае, когда равны между собой рациональные слагаемые обеих частей и коэффициенты при одинаковых радикалах. Таким образом, получаются четыре уравнения для нахождения неизвестных коэффициентов a , b , c и d :

a - 2 b + 3c = 1

- a + b +3 d = 1

a + c - 2 d = - 1

b - c + d = 0 , откуда a = 0 ; b = - ; c = 0 ; d = , то есть
= -
+
.

Глава II . Поиски решения задач с многочленами методом неопределенных коэффициентов .

«Ничто так не содействует усвоению предме-

та, как действие с ним в разных ситуациях »

Академик Б.В.Гнеденко

2. 1.Разложение многочлена на множители.

Способы разложения многочленов на множители:

1) вынесение общего множителя за скобки;2) метод груп- пировки; 3) применение основных формул умножения; 4) введение вспомогательных членов;5)предварительное преобразование данного многочлена с помощью тех или иных формул; 6) разложение с помощью отыскания корней данного многочлена; 7) метод введения параметра; 8)метод неопределенных коэффициентов.

З а д а ч а 1. Разложить на действительные множители многочлен х 4 + х 2 + 1 .

Решение. Среди делителей свободного члена данного многочлена нет корней. Другими элементарными средствами корни многочлена найти не можем. Поэтому выполнить требуемое разложение с помощью предварительного отыскания корней данного многочлена не представляется возможным. Остается искать решение задачи либо методом введения вспомогательных членов, либо методом неопределенных коэффициентов. Очевидно, что х 4 + х 2 + 1 = х 4 + х 3 + х 2 - х 3 - х 2 - х + х 2 + х + 1 =

= х 2 (х 2 + х + 1) - х (х 2 + х + 1) + х 2 + х + 1 =

= (х 2 + х + 1)( х 2 - х + 1).

Полученные квадратные трёхчлены не имеют корней, а потому неразложимы на действительные линейные множители.

Изложенный способ технически прост, но труден вследствие своей искусственности. Действительно, очень трудно придумать требующиеся вспомогательные члены. Найти это разложение нам помогла всего лишь догадка. Но

существуют и более надёжные способы решения таких задач.

Можно было бы действовать так: предположить, что данный многочлен разлагается в произведение

(х 2 + а х + b )( х 2 + c х + d )

двух квадратных трёхчленов с целыми коэффициентами.

Таким образом, будем иметь, что

х 4 + х 2 + 1 = (х 2 + а х + b )( х 2 + c х + d )

Остается определить коэффициенты a , b , c и d .

Перемножив многочлены, стоящие в правой части последнего равенства, получим: х 4 + х 2 + 1 = х 4 +

+ (а + с ) х 3 + (b + а c + d ) х 2 + (ad + bc ) х + bd .

Но поскольку нам необходимо, чтобы правая часть этого равенства превратилась в такой же многочлен, который стоит в левой части, потребуем выполнения следующих условий:

а + с = 0

b + а c + d = 1

ad + bc = 0

bd = 1 .

Получилась система четырех уравнений с четырьмя неизвестными a , b , c и d . Легко найти из этой системы коэффициенты a = 1 , b = 1 , c = -1 и d = 1.

Теперь задача решена полностью. Мы получили:

х 4 + х 2 + 1 = (х 2 + х + 1)( х 2 - х + 1).

З а д а ч а 2. Разложить на действительные множители многочлен х 3 – 6 х 2 + 14 х – 15 .

Решение. Представим данный многочлен в виде

х 3 – 6 х 2 + 14 х – 15 = (х + а )(х 2 + bx + c ) , где a , b и с - не определённые пока коэффициенты. Так как два многочлена тождественно равны тогда и только тогда, когда коэффициенты при одинаковых степенях х равны, то, приравнивая коэффициенты соответственно при х 2 , х и свободные члены, получим систему трёх уравнений с тремя неизвестными:

a + b = - 6

ab + c = 14

ac = - 15 .

Решение этой системы значительно упростится, если учесть, что число 3 (делитель свободного члена) является корнем данного уравнения, и, следовательно, a = - 3 ,

b = - 3 и с = 5 .

Тогда х 3 – 6 х 2 + 14 х – 15 = (х – 3)(х 2 – 3 x + 5).

Примененный метод неопределенных коэффициентов по сравнению с изложенным выше методом введения вспомогательных членов не содержит ничего искусственного, но зато требует применения многих теоретических положений и сопровождается довольно большими выкладками. Для многочленов более высокой степени такой метод неопределенных коэффициентов приводит к громоздким системам уравнений.

2.2.Задачи с параметрами.

В последние годы в вариантах ЕГЭ предлагаются задачи с параметрами. Их решение часто вызывает определенные трудности. При решении задач с параметрами наряду с другими методами можно достаточно эффективно применить метод неопределенных коэффициентов. Именно данный метод позволяет намного упростить их решение и быстро получить ответ.

З а д а ч а 3. Определите, при каких значениях параметра а уравнение 2х 3 – 3 х 2 – 36 х + а – 3 = 0 имеет ровно два корня.

Решение. 1 способ. С помощью производной.

Представим данное уравнение в виде двух функций

2х 3 – 3 х 2 – 36 х – 3 = – а .

f (x ) = 2х 3 – 3 х 2 – 36 х – 3 и φ(х ) = – а .

Исследуем функцию f (x ) = 2х 3 – 3 х 2 – 36 х – 3 при помощи производной и построим схематически ее график (рис. 1.).

f( – x ) f (x ) , f (– x ) – f (x ). Функция не является четной и не является нечетной.

3. Найдем критические точки функции, ее промежутки возрастания и убывания, экстремумы. f / (x ) = 6 x 2 – 6 х – 36. D (f / ) = R , поэтому все критические точки функции найдем, решив уравнение f / (x ) = 0 .

6(х 2 – х – 6) = 0 ,

х 2 – х – 6 = 0 ,

х 1 = 3 , х 2 = – 2 по теореме, обратной теореме Виета.

f / (x ) = 6(х – 3)(х + 2).

+ max - min +

2 3 x

f / (x ) > 0 при всех х < – 2 и х > 3 и функция непрерывна в точках х = – 2 и х = 3 , следовательно, она возрастает на каждом из промежутков (-; - 2] и [ 3 ; ).

f / (x ) < 0 при - 2 < х < 3 , следовательно, она убывает на промежутке [- 2 ; 3 ].

х = - 2 точка максимума, т.к. в этой точке знак производной изменяется с « + » на « – » .

f (– 2) = 2· (– 8) – 3·4 – 36·(– 2) – 3 = – 16 – 12 + 72 – 3 = = 72 – 31 = 41 ,

х = 3 точка минимума, так как в этой точке знак производной изменяется « – » на « + » .

f (3) = 2·27 – 3·9 – 36·3 – 3 = 54 – 27 – 108 – 3 = – 138 + +54 = – 84 .

График функции φ(х ) = – а есть прямая, параллельная оси абсцисс и проходящая через точку с координатами (0 ; – а ). Графики имеют две общие точки при – а = 41 , т.е. а = – 41 и – а = – 84 , т.е. а = 84 .

у

41 φ(х )

2 3 х

3 f ( x ) = 2х 3 – 3 х 2 – 36 х – 3

2 способ. Методом неопределенных коэффициентов.

Так как по условию задачи данное уравнение должно иметь всего лишь два корня, то очевидно выполнение равенства:

2х 3 – 3 х 2 – 36 х + а – 3 = (х + b ) 2 (2 x + c ) ,

2х 3 – 3 х 2 – 36 х + а – 3 = 2 x 3 + (4 b + c ) x 2 + (2 b 2 + +2 bc ) x + b 2 c ,

Теперь приравнивая коэффициенты при одинаковых степенях х , получим систему уравнений

4 b + c = - 3

2b 2 + 2bc = - 36

b 2 c = a – 3 .

Из первых двух уравнений системы найдем b 2 + b – 6 = 0, откуда b 1 = - 3 или b 2 = 2 . Соответственные значения с 1 и с 2 легко найти из первого уравнения системы: с 1 = 9 или с 2 = - 11 . Окончательно, искомое значение параметра, можно определить из последнего уравнения системы:

а = b 2 c + 3 , a 1 = - 41 или a 2 = 84.

О т в е т: данное уравнение имеет ровно два различных

корня при а = - 41 и а = 84 .

З а д а ч а 4 .Найдите наибольшее значение параметра а , при котором уравнение х 3 + 5 х 2 + ах + b = 0

с целыми коэффициентами имеет три различных корня, один из которых равен – 2 .

Решение. 1 способ. Подставив х = - 2 в левую часть уравнения, получим

8 + 20 – 2 а + b = 0, а значит, b = 2 a – 12 .

Так как число – 2 является корнем, то можно вынести общий множитель х + 2:

х 3 + 5 х 2 + ах + b = х 3 + 2 х 2 + 3 х 2 + ах + (2 a – 12) =

= x 2 (х + 2) + 3 x (х + 2) – 6 x + ах + (2 a – 12) =

= x 2 (х + 2) + 3 x (х + 2) + (a – 6)(x +2) - 2(a – 6)+ (2 a – 12) =

= (х + 2)(х 2 + 3 x + (a – 6) ) .

По условию имеются еще два корня уравнения. Значит, дискриминант второго множителя положителен.

D =3 2 - 4 (a – 6) = 33 – 4 a > 0 , то есть а < 8,25 .

Казалось бы, что ответом будет а = 8 . Но при подстановке числа 8 в исходное уравнение получаем:

х 3 + 5 х 2 + ах + b = х 3 + 5 х 2 + 8 х + 4 = (х + 2)(х 2 + 3 x + 2 ) =

= (х + 1) (х + 2) 2 ,

то есть уравнение имеет только два различных корня. А вот при а = 7 действительно получается три различных корня.

2 способ. Метод неопределенных коэффициентов.

Если уравнение х 3 + 5 х 2 + ах + b = 0 имеет корень х = - 2, то всегда можно подобрать числа c и d так, чтобы при всех х было верно равенство

х 3 + 5 х 2 + ах + b = (х + 2)(х 2 + с x + d ).

Для нахождения чисел c и d раскроем скобки в правой части, приведем подобные члены и получим

х 3 + 5 х 2 + ах + b = х 3 + (2 + с ) х 2 +(2 с + d ) х + 2 d

Приравнивая коэффициенты при соответствующих степенях х имеем систему

2 + с = 5

2 с + d = a

2 d = b , откуда с = 3 .

Следовательно, х 2 + 3 x + d = 0 , D = 9 – 4 d > 0 или

d < 2,25 , итак d (- ; 2 ].

Условию задачи удовлетворяет значение d = 1 . Окончательно искомое значение параметра а = 7.

О т в е т: при а = 7 данное уравнение имеет три различных корня.

2.3. Решение уравнений.

«Помните, что решая маленькие задачи, вы

готовите себя к решению больших и труд-

ных задач.»

Академик С.Л.Соболев

При решении некоторых уравнений можно и нужно проявить находчивость и остроумие, применять специальные приемы. Владение разнообразными приемами преобразований и умение проводить логические рассуждения имеет в математике большое значение. Один из этих приемов состоит в том, чтобы прибавить и вычесть некоторые удачно подобранное выражение или число. Сам по себе сформулированный факт, конечно, хорошо всем известен - основная трудность состоит в том, чтобы увидеть в конкретной конфигурации те преобразования уравнений, к которым его удобно и целесообразно применить.

На простом алгебраическом уравнении проиллюстрируем один нестандартный прием решения уравнений.

З а д а ч а 5. Решить уравнение

=
.

Решение. Умножим обе части данного уравнения на 5 и перепишем следующим образом

= 0 ; х 0; -
;

= 0 ,

= 0 ,

= 0 или
= 0

Полученные уравнения решим методом неопределенных коэффициентов

х 4 - х 3 –7 х – 3 = (х 2 + ах + b )(x 2 + cx + d ) = 0

х 4 - х 3 –7 х – 3 = х 4 + (а + с ) х 3 + (b + а c + d ) х 2 + (ad + bc ) х+ + bd

Приравнивая коэффициенты при х 3 , х 2 , х и свободные члены, получим систему

а + с = -1

b + а c + d = 0

ad + bc = -7

bd = -3 , откуда находим: а = -2 ; b = - 1 ;

с = 1 ; d = 3 .

Итак х 4 - х 3 –7х – 3 = (х 2 – 2 х – 1)(х 2 + х + 3) = 0 ,

х 2 – 2 х – 1 = 0 или х 2 + х + 3 = 0

х 1,2 =
нет корней.

Аналогично имеем

х 4 – 12х – 5 = (х 2 – 2 х – 1)(х 2 + 2х + 5) = 0 ,

откуда х 2 + 2 х + 5 = 0 , D = - 16 < 0 , нет корней.

О т в е т: х 1,2 =

З а д а ч а 6. Решить уравнение

= 10.

Решение. Для решения данного уравнения необходимо подобрать числа а и b таким образом, чтобы числители обеих дробей были одинаковыми. Следовательно, имеем систему:

= 0 , х 0; -1 ; -

= - 10

Таким образом, задача заключается в том, чтобы подобрать числа а и b , для которых выполняется равенство

(а + 6) х 2 + ах – 5 = х 2 + (5 + 2 b ) x + b

Теперь, согласно теореме о равенстве многочленов, необходимо, чтобы правая часть этого равенства превратилась в такой же многочлен, который стоит в левой части.

Иначе говоря, должны выполняться соотношения

а + 6 = 1

а = 5 + 2 b

– 5 = b , откуда находим значения а = - 5 ;

b = - 5 .

При этих значениях а и b равенство а + b = - 10 тоже справедливо.

= 0 , х 0; -1 ; -

= 0 ,

= 0 ,

(х 2 – 5х – 5)(х 2 + 3х + 1) = 0 ,

х 2 – 5х – 5 = 0 или х 2 + 3х + 1 = 0 ,

х 1,2 =
, х 3,4 =

О т в е т: х 1,2 =
, х 3,4 =

З а д а ч а 7. Решить уравнение

= 4

Решение. Данное уравнение сложнее предыдущих и поэтому сгруппируем таким образом, х 0;-1;3;-8;12

0 ,

= - 4.

Из условия равенства двух многочленов

ах 2 + (а + 6) х + 12 = х 2 + (b + 11) x – 3 b ,

получим и решим систему уравнений относительно неизвестных коэффициентов а и b :

а = 1

а + 6 = b + 11

12 = – 3 b , откуда а = 1 , b = - 4 .

Многочлены - 3 – 6 х + сх 2 + 8 сх и х 2 + 21 + 12 d – dx равны друг другу тождественно лишь тогда, когда

с = 1

8 с – 6 = - d

3 = 21 + 12 d , с = 1 , d = - 2 .

При значениях а = 1 , b = - 4 , с = 1 , d = - 2

равенство
= - 4 справедливо.

В результате данное уравнение принимает следующий вид:

= 0 или
= 0 или
= 0 ,

= - 4 , = - 3 , = 1 , = -
.

Из рассмотренных примеров видно, как умелое использование метода неопределенных коэффициентов,

помогает упростить решение довольно сложного, необычного уравнения.

2.4. Функциональные уравнения.

«Высшее назначение математики... состоит

в том, чтобы находить скрытый порядок в

хаосе, который нас окружает»

Н.Винер

Функциональные уравнения-весьма общий класс уравнений, в которых искомой является некоторая функция. Под функциональным уравнением в узком смысле слова понимают уравнения, в которых искомые функции связаны с известными функциями одного или нескольких переменных при помощи операции образования сложной функции. Функциональное уравнение можно также рассматривать как выражение свойства, характеризующего тот или иной класс функций

[ например, функциональное уравнение f ( x ) = f (- x ) характеризует класс четных функций, функциональное уравнение f (x + 1) = f (x ) – класс функций, имеющих период 1, и т.д. ].

Одним из простейших функциональных уравнений является уравнение f (x + y ) = f (x ) + f (y ). Непрерывные решения этого функционального уравнения имеют вид

f (x ) = C x . Однако в классе разрывных функций это функциональное уравнение имеет и иные решения. С рассмотренным функциональным уравнением связаны

f (x + y ) = f (x ) · f (y ), f (x y ) = f (x ) + f (y ), f (x y ) = f (x )· f (y ),

непрерывные решения, которых, имеют соответственно вид

е сх , С ln x , x α (x > 0).

Таким образом, эти функциональные уравнения могут служить для определения показательной, логарифмической и степенной функций.

Наибольшее распространение получили уравнения, в сложных функциях которых искомыми являются внешние функции. Теоретические и практические применения

именно таких уравнений побуждали выдающихся математиков к их изучению.

Так, например,у равнение

f 2 (x ) = f (x - y )· f (x + y )

Н.И.Лобачевский использовал при определении угла параллельности в своей геометрии.

В последние годы задачи, связанные с решением функциональных уравнений, довольно часто предлагают на математических олимпиадах. Их решение не требует знаний, выходящих за рамки программы по математике общеобразовательных школ. Однако решение функциональных уравнений часто вызывает определенные затруднения.

Одним из способов нахождения решений функциональных уравнений является метод неопределенных коэффициентов. Его можно применять тогда, когда по внешнему виду уравнения можно определить общий вид искомой функции. Это относится, прежде всего, к тем случаям, когда решения уравнений следует искать среди целых или дробно-рациональных функций.

Изложим суть этого приема, решая следующие задачи.

З а д а ч а 8. Функция f (x ) определена при всех действительных х и удовлетворяет при всех х R условию

3 f (x ) - 2 f (1- x ) = x 2 .

Найдите f (x ).

Решение. Так как в левой части данного уравнения над независимой переменной х и значениями функции f выполняются только линейные операции, а правая часть уравнения - квадратичная функция, то естественно предположить, что искомая функция также квадратичная:

f (х ) = ax 2 + bx + c , где a , b , c – коэффициенты, подлежащие определению, то есть неопределенные коэффициенты.

Подставляя функцию в уравнение, приходим к тождеству:

3(ax 2 + bx + c ) – 2(a (1 – x ) 2 + b (1 – x ) + c ) = x 2 .

ax 2 + (5 b + 4 a ) x + (c – 2 a – 2 b ) = x 2 .

Два многочлена будут тождественно равны, если равны

коэффициенты при одинаковых степенях переменной:

a = 1

5b + 4a = 0

c – 2 a – 2 b = 0.

Из этой системы находим коэффициенты

a = 1 , b = - , c = , также удовлетворяет равенству

3 f (x ) - 2 f (1- x ) = x 2 на множестве всех действительных чисел. При этом существует такое x 0 З а д а ч а 9. Функция у = f (x ) при всех х определена, непрерывна и удовлетворяет условию f (f (x )) – f (x ) = 1 + 2 x . Найдите две такие функции.

Решение. Над искомой функцией выполняются два действия – операция составления сложной функции и

вычитание. Учитывая, что правая часть уравнения – линейная функция, естественно предположить, что искомая функция тоже линейная: f (x ) = ах + b , где а и b – неопределённые коэффициенты. Подставив эту функцию в f (f ( (x ) = - х - 1 ;

f 2 (x ) = 2 х + , являющиеся решениями функционального уравнения f (f (x )) – f (x ) = 1 + 2 x .

Заключение.

В заключении необходимо отметить, что эта работа безусловно будет способствовать дальнейшему изучению оригинального и эффективного метода решения разнообразных математических задач, которые являются задачами повышенной трудности и требует глубокого знания школьного курса математики и высокой логической культуры.Все желающие самостоятельно углубить свои знания по математике, также найдут в данной работе материал для размыщлений и интересные задачи, решение которых принесет пользу и удовлетворение.

В работе в рамках существующей школьной программы и в форме, доступной для эффективного восприятия изложен метод неопределенных коэффициентов, способствующий углублению школьного курса математики.

Конечно, все возможности метода неопределенных коэффициентов нельзя показать в одной работе. В самом деле метод еще требует дальнейшего изучения и исследования.

Список использованной литературы.

Глейзер Г.И..История математики в школе.-М.: Просвещение, 1983.

Гомонов С.А. Функциональные уравнения в школьном курсе математики // Математика в школе. – 2000 . – №10 .

Дорофеев Г.В., Потапов М.К., Розов Н.Х.. Пособие по математике.- М. : Наука, 1972 .

Курош А.Г.. Алгебраические уравнения произвольных степеней.-М.: Наука, 1983.

Лихтарников Л.М.. Элементарное введение в функциональные уравнения. – СПб. : Лань, 1997 .

Мантуров О.В., Солнцев Ю.К., Сорокин Ю.И., Федин Н.Г..Толковый словарь математических терминов.-М.:Просвещение,1971

Моденов В.П.. Пособие по математике. Ч.1.-М.: МГУ, 1977.

Моденов В.П.. Задачи с параметрами.-М.: Экзамен, 2006.

Потапов М.К., Александров В.В.,Пасиченко П.И.. Алгебра и анализ элементарных функций.- М. : Наука, 1980.

ХалиуллинА.А.. Можно решать проще // Математика в школе. – 2003 . - №8 .

Халиуллин.

4. Разложить многочлен 2 х 4 – 5х 3 + 9х 2 – 5х + 3 на множители с целыми коэффициентами.

5. При каком значении а х 3 + 6х 2 + ах + 12 на х + 4 ?

6. При каком значении параметра а уравнение х 3 +5 х 2 + + ах + b = 0 с целыми коэффициентами имеет два различных корня,один из которых равен 1?

7. Среди корней многочлена х 4 + х 3 – 18х 2 + ах + b с целыми коэффициентами имеются три равных целых числа. Найдите значение b .

8. Найдите наибольшее целое значение параметра а, при котором уравнение х 3 – 8х 2 + ах + b = 0 с целыми коэффициентами имеет три различных корня, один из которых равен 2.

9. При каких значениях а и b выполняется без остатка делениех 4 + 3х 3 – 2х 2 + ах + b на х 2 – 3х + 2 ?

10. Разложить многочлены на множители:

а) х 4 + 2 х 2 – х + 2 в) х 4 – 4х 3 +9х 2 –8х + 5 д) х 4 + 12х – 5

б) х 4 + 3х 2 + 2х + 3 г) х 4 – 3х –2 е) х 4 – 7х 2 + 1 .

11. Решите уравнения:

а)
= 2 = 2 f (1 – х ) = х 2 .

Найдите f (х ) .

13. Функция у = f (х ) при всех х определена, непрерывна и удовлетворяет условию f ( f (х )) = f (х ) + х. Найдите две такие функции.

Метод применим для минимизации функций алгебры логики от любого числа переменных.

Рассмотрим случай трех переменных. Булева функция в ДНФ может быть представлена в виде всевозможных конъюнктивных членов, которые могут входить в ДНФ:

где kÎ{0,1} ‑ коэффициенты. Метод заключается в подборе коэффициентов таким образом, чтобы получаемая ДНФ была минимальной.

Если теперь задать всевозможные значения переменных от 000 до 111, то получим 2 n (2 3 =8) уравнений для определения коэффициентов k :

Рассматривая наборы, на которых функция принимает нулевое значение, определяют коэффициенты, которые равны 0, и вычеркивают их из уравнений, в правой части которых стоит 1. Из оставшихся коэффициентов в каждом уравнении к единице приравнивают по одному коэффициенту, определяющему конъюнкцию наименьшего ранга. Остальные коэффициенты приравнивают к 0. Итак, единичные коэффициенты k определяют соответствующую минимальную форму.

Пример . Минимизировать заданную функцию

если известны значения:
;
;
;
;
;
;
;
.

Решение.

После вычеркивания нулевых коэффициентов получим:

=1;

=1;

=1;

=1.

Приравняем к единице коэффициент , соответствующий конъюнкции наименьшего ранга и обращающий четыре последних уравнения в 1, а в первом уравнении целесообразно приравнять к 1 коэффициент. Остальные коэффициенты приравнивают к 0.

Ответ : вид минимизированной функции .

Следует отметить, что метод неопределенных коэффициентов эффективен, когда число переменных невелико и не превышает 5-6.

Многомерный куб

Рассмотрим графическое представление функции в виде многомерного куба. Каждой вершине n -мерного куба можно поставить в соответствие конституенту единицы.

Подмножество отмеченных вершин является отображением на n -мерном кубе булевой функции от n переменных в СДНФ.

Для отображения функции от n переменных, представленной в любой ДНФ, необходимо установить соответствие между ее минитермами и элементами n -мерного куба.

Минитерм (n-1)-го ранга
можно рассматривать как результат склеивания двух минитермовn -го ранга, т.е.

=

На n -мерном кубе это соответствует замене двух вершин, которые отличаются только значениями координат х i , соединяющих эти вершины ребром (говорят, что ребро покрывает инцидентные ему вершины).

Таким образом, минитермам (n -1)-го порядка соответствуют ребра n-мерного куба.

Аналогично устанавливается соответствие минитермов (n -2)-го порядка граням n -мерного куба, каждая из которых покрывает четыре вершины (и четыре ребра).

Элементы n -мерного куба, характеризующиеся S измерениями, называются S -кубами.

Так вершины являются 0-кубами, ребра 1-кубами, грани 2-кубами и т.д.

Обобщая, можно сказать, что минитерм (n-S ) ранга в ДНФ для функции n переменных отображается S -кубом, причем каждый S -куб покрывает все те кубы низшей размерности, которые связаны только с его вершинами.

Пример. На рис. дано отображение

Здесь минитермы
и
соответствуют 1-кубам (S =3-2=1), а минитерм х 3 отображается 2-кубам (S =3-1=2).

Итак, любая ДНФ отображается на n -мерном кубе совокупностью S -кубов, которые покрывают все вершины, соответствующие конституентам единицам (0-куба).

Конституенты . Для переменных х 1 , х 2 ,… х n выражение
называют конституентой единицы, а
- конституентой нуля (означает либо, либо).

Данная конституента единицы (нуля) обращается в единицу (нуль) только при одном соответствующем ей наборе значений переменных, который получается, если все переменные принять равными единице (нулю), а их отрицания - нулю (единице).

Например: конституенте единице
соответствует набор (1011), а конституенте нуля
- набор (1001).

Так как СД(К)НФ является дизъюнкцией (конъюнкцией) конституент единицы (нуля), то можно утверждать, что представляемая ею булева функция f (x 1 , x 2 ,…, x n ) обращается в единицу (нуль) только при наборах значений переменных x 1 , x 2 ,…, x n , соответствующих этим копституантам. На остальных наборах эта функция обращается в 0 (единицу).

Справедливо и обратное утверждение, на котором основан способ представления в виде формулы любой булевой функции, заданной таблицей.

Для этого необходимо записать дизъюнкции (конъюнкции) конституент единицы (нуля), соответствующих наборам значений переменных, на которых функция принимает значение, равное единице (нулю).

Например, функции, заданной таблицей

соответствуют

Полученные выражения можно преобразовать к другому виду на основании свойств алгебры логики.

Справедливо и обратное утверждение: если некоторая совокупность S -кубов покрывает множество всех вершин, соответствующих единичным значениям функции, то дизъюнкция соответствующих этим S -кубам минитермов является выражением данной функции в ДНФ.

Говорят, что такая совокупность S -кубов (или соответствующих им минитермов) образует покрытие функции. Стремление к минимальной форме интуитивно понимается как поиск такого покрытия, число S -кубов которого было бы поменьше, а их размерность S - побольше. Покрытие, соответствующее минимальной форме, называют минимальным покрытием.

Например, для функции у =
покрытие соответствует неминимальной форме:

рис a) у =,

а покрытия на рис б) у =
, рис в) у =
минимальные.

Рис. Покрытие функции у =:

а) неминимальное; б), в) минимальное.

Отображение функции на n -мерном наглядно и просто при n 3. Четырехмерный куб можно изобразить, как показано на рис., где отображены функции четырех переменных и ее минимальное покрытие, соответствующее выражению у =

Использование этого метода при n >4 требует настолько сложных построений, что теряет все его преимущества.

Равенство (I) есть тождество. Приведя его к целому виду, получим равенство 2-х многочленов. Но такое равенство всегда выполняется лишь при условии почленного равенства этих многочленов.

Приравнивая коэффициенты при одинаковых степенях х, стоящих в левой и правой частях равенства, получим систему линейных уравнений относительно неизвестных коэффициентов, которую надлежит решить.

Так как разложение (I) всегда существует для любой правильной рациональной дроби, то полученная система всегда совместна.

Такой метод нахождения коэффициентов называется методом неопределенных коэффициентов (способ сравнения коэффициентов).

Приведем пример разложения рациональной функции на элементарные дроби.

Пример 6.6.27. Разложить дробь на элементарные.

последнее уравнение подставим во второе

Таким образом,
.

x=2 ;

x=3 .

Следует; .

Метод частных значений требует меньших затрат труда и поэтому заслуживает особого внимания при интегрировании рациональных дробей.

Если корни знаменателя только действительные, то для определения неизвестных коэффициентов целесообразно пользоваться именно этим способом.

В остальных случаях для определения неизвестных коэффициентов можно комбинировать оба способа.

Замечание. Метод частных значений применяется и тогда, когда другие случаи, но здесь нужно тождество дифференцировать.

Таким образом, для интегрирования правильных рациональных дробей достаточно уметь:

1) интегрировать элементарные дроби;

2) разлагать рациональные дроби на элементарные.

3. Интегрирование рациональных дробей

Схема интегрирования рациональных дробей:

Для интегрирования рациональных дробей ;

Где P(x) и Q(x) – многочлены с действительными коэффициентами, последовательно выполняют три шага.

Первый шаг. Если дробь неправильная, то есть степень числителя P(x) больше или равна степени знаменателя Q(x), выделяют целую часть рациональной дроби, деля числитель на знаменатель по правилу деления многочлена на многочлен. После этого рациональная дробь может быть записана в виде суммы:

1) выделенной целой части – многочлена М(х);

2) правильной остаточной дроби :

Второй шаг.

Правильную остаточную дробь разлагают на последующие дроби.

Для этого находят корни уравнения Q(x)=0 и разлагают знаменатель Q(x) на множители первой и второй степени с действительными коэффициентами:

В этом разложении знаменателя множители 1-й степени соответствуют действительным корням, а множители 2-й степени – параллельных сопряженных корней.

Коэффициент при большей степени х в знаменателе Q(x) можно считать равным 1 ибо этого всегда можно добиться, делением на него P(x) и Q(x).

После этого правильная остаточная дробь разлагается на простейшие (элементарные).

Третий шаг. Находят интегралы выделенной целой части и всех элементарных дробей (методами, рассмотренными выше), которые затем складывают.

Пример6.6.28.

Под знаком интеграла – неправильная рациональная дробь, так как степень числитель равна степени знаменателя, поэтому выделяем целую часть.

Рациональная функция - это дробь вида , числитель и знаменатель которой - многочлены или произведения многочленов.

Пример 1. Шаг 2.

.

Умножаем неопределённые коэффициенты на многочлены, которых нет в данной отдельной дроби, но которые есть в других полученных дробях:

Раскрываем скобки и приравниваем полученое к полученному выражению числитель исходной подынтегральной дроби:

В обеих частях равенства отыскиваем слагаемые с одинаковыми степенями икса и составляем из них систему уравнений:

.

Сокращаем все иксы и получаем эквивалентную систему уравнений:

.

Таким образом, окончательное разложение подынтегральной дроби на сумму простых дробей:

.

Пример 2. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

.

Теперь начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю выражения, полученного после приведения суммы дробей к общему знаменателю:

Теперь требуется составить и решить систему уравнений. Для этого приравниваем коэффициенты при переменной в соответствующей степени в числителе исходного выражения функции и аналогичные коэффициенты в полученном на предыдущем шаге выражения:

Решаем полученную систему:

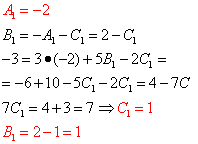
Итак, , отсюда

.

Пример 3. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю выражения, полученного после приведения суммы дробей к общему знаменателю:

Как и в предыдущих примерах составляем систему уравнений:

Сокращаем иксы и получаем эквивалентную систему уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

.

Пример 4. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

.

Как приравнивать числитель исходной дроби к выражению в числителе, полученному после разложения дроби на сумму простых дробей и приведения этой суммы к общему знаменателю, мы уже знаем из предыдуших примеров. Поэтому лишь для контроля приведём получившуюся систему уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

Пример 5. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

.

Самостоятельно приводим к общему знаменателю эту сумму, приравнивать числитель этого выражения к числителю исходной дроби. В результате должна получиться следующая система уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

.

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

.

Пример 6. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Производим с этой суммой те же действия, что и в предыдущих примерах. В результате должна получиться следующая система уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

.

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

.

Пример 7. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

.

После известных действий с полученной суммой должна получиться следующая система уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

.

Пример 8. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

.

Внесём некоторые изменения в уже доведённые до автоматизма действия для получения системы уравнений. Есть искусственный приём, который в некоторых случаях помогает избежать лишних вычислений. Приводя сумму дробей к общему знаменателю получаем и приравнивая числитель этого выражения к числителю исходной дроби, получаем.