Несобственные интегралы 2 рода. Как вычислить несобственный интеграл и выяснить его сходимость

Лекция 24. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

План:

1. Понятие несобственного интеграла
2. Несобственные интегралы I рода.
3. Несобственные интегралы II рода.

1. Понятие несобственного интеграла

Рассмотрим нахождение обоих видов несобственных интегралов.

Пусть задана функция y=f(x) , непрерывная на промежутке [a;+∞ ). Если существует конечный предел , то его называют несобственным интегралом первого рода и обозначают .

сходится расходится .

Геометрический смысл несобственного интеграла I рода заключается в следующем: если сходится (при условии, что f(x) ≥0), то он представляет собой площадь "бесконечно длинной" криволинейной трапеции (рис. 24.1).

Аналогично вводится понятие несобственного интеграла с бесконечным нижним пределом интегрирования для непрерывной на промежутке (-∞ ;b ] функции: = .

Несобственный интеграл с двумя бесконечными пределами интегрирования определяется формулой: = + , где с – произвольное число.

Рассмотрим примеры нахождения несобственных интегралов I рода.

Пример 24.1.

Решение . Для нахождения несобственного интеграла с бесконечной верхней границей от непрерывной функции воспользуемся формулой: = . Тогда = . Сначала вычислим интеграл от е х :

= = = =∞. Получили, что несобственный интеграл расходится.

Ответ : расходится.

Пример 24.2. Вычислите несобственный интеграл или установите его расходимость: .

Решение . Подынтегральная функция непрерывна на промежутке (-∞ ;- 1]. Для нахождения несобственного интеграла I рода с бесконечной нижней границей воспользуемся формулой: = . Тогда = . Вычислим интеграл, содержащийся под знаком предела: = . Избавимся от знака "минус", поменяв границы интегрирования местами:

1. Получили, что рассматриваемый несобственный интеграл сходится.

Ответ : =1.

1. Несобственные интегралы II рода.

Пусть задана функция y=f(x) , непрерывная на промежутке [a;b ). Пусть b – точка разрыва второго рода. Если существует конечный предел , то его называют несобственным интегралом второго рода и обозначают .

Таким образом, по определению = .

Если найденный предел равен конечному числу, то говорят, что несобственный интеграл сходится . Если указанный предел не существует или бесконечен, то говорят, что интеграл расходится .

Геометрический смысл несобственного интегралаII рода , где b – точка разрыва второго рода, f(x) ≥0, заключается в следующем: если сходится, то он представляет собой площадь "бесконечно высокой" криволинейной трапеции (рис. 24.2).

Аналогично вводится понятие несобственного интеграла II рода для непрерывной на промежутке (a;b ]функции при условии, что а – точка разрыва второго рода: = .

Пример 24.3. Вычислите несобственный интеграл II рода: .

Решение . Подынтегральная функция непрерывна на промежутке (0;1], причем х= 0 - точка разрыва второго рода (). Для вычисления несобственного интеграла воспользуемся формулой: = . Получим, что

= = = = = = ∞. Видим, что несобственный интеграл II рода расходится.

Ответ : расходится.

Контрольные вопросы:

1. Что называют несобственным интегралом?
2. Какие интегралы называются несобственными интегралами первого рода?
3. В чем заключается геометрический смысл несобственного интеграла первого рода?
4. Какие несобственные интегралы называют сходящимися, а какие расходящимися?
5. Какие интегралы называются несобственными интегралами второго рода?
6. В чем заключается геометрический смысл несобственного интеграла второго рода?

СПИСОК ЛИТЕРАТУРЫ:

1. Абдрахманова И.В. Элементы высшей математики: учеб. пособие – М.: Центр интенсивных технологий образования, 2003. – 186 с.

2. Алгебра и начала анализа (Ч.1, Ч.2): Учебник для ССУЗов / под ред. Г.Н.Яковлева. – М.: Наука, 1981.

3. Александрова Н.В. Математические термины. Справочник.- М.: Высш. школа, 1978. - 190 с.

4. Валуце И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы: Учеб. пособие. – М.: Наука, 1989. – 576 с.

5. Григорьев В.П., Дубинский Ю.А. Элементы высшей математики: Учеб. для студ. учреждений СПО. - М.: Издательский центр "Академия", 2004. – 320с.

6. Лисичкин В.Т., Соловейчик И.Л. Математика: учеб. пособие для техникумов. – М.: Высш. школа, 1991. – 480 с.

7. Луканкин Г.Л., Мартынов Н.Н., Шадрин Г.А., Яковлев Г.Н. Высшая математика: учеб. пособие для студентов пед. институтов. – М.: Просвещение, 1988. – 431 с.

8. Письменный Д.Т. Конспект лекций по высшей математике: Ч.1. – М.:Айрис-пресс, 2006.- 288 с.

9. Филимонова Е.В. Математика: учеб. пособие для ссузов. – Ростов н/Д: Феникс, 2003. – 384 с.

10. Шипачев В.С. Высшая математика: учебник для вузов. – М.: Высшая школа, 2003. – 479 с.

11. Шипачев В.С. Курс высшей математики: высшее образование. – М.: ПРОЮЛ М.А.Захаров, 2002. – 600 с.

12. Энциклопедия для детей. Т.11. Математика / Глав. ред. М.В.Аксенова. - М.: Аванта+, 2000.- 688 с.

Если подинтегральная функция имеет на (конечном) интервале интегрирования разрыв второго рода, говорят о несобственном интеграле второго рода.

10.2.1 Определение и основные свойства

Обозначим интервал интегрирования $\left[ a, \, b \right ]$, оба этих числа ниже полагаются конечными. Если имеется всего 1 разрыв, он может находиться или в точке $a$, или в точке $b$, или внутри интервала $(a,\,b)$. Рассмотрим сначала случай, когда разрыв второго рода имеется в точке $a$, а в остальных точках подинтегральная функция непрерывна. Итак, мы обсуждаем интеграл

\begin{equation} I=\int _a^b f(x)\,dx, (22) \label{intr2} \end{equation}

причем $f(x) \rightarrow \infty $, когда $x \rightarrow a+0$. Как и ранее, прежде всего следует придать смысл этому выражению. Для этого рассмотрим интеграл

\[ I(\epsilon)=\int _{a+\epsilon}^b f(x)\,dx. \]

Определение. Пусть существует конечный предел

\[ A=\lim _{\epsilon \rightarrow +0}I(\epsilon)=\lim _{\epsilon \rightarrow +0}\int _{a+\epsilon}^b f(x)\,dx. \]

Тогда говорят, что несобственный интеграл второго рода (22) сходится, и ему приписывают значение $A$, саму функцию $f(x)$ называют интегрируемой на интервале $\left[ a, \, b\right]$.

Рассмотрим интеграл

\[ I=\int ^1_0\frac{dx}{\sqrt{x}}. \]

Подинтегральная функция $1/\sqrt{x}$ при $x \rightarrow +0$ имеет бесконечный предел, так что в точке $x=0$ она имеет разрыв второго рода. Положим

\[ I(\epsilon)=\int ^1_{\epsilon }\frac{dx}{\sqrt{x}}\,. \]

В данном случае первообразная известна,

\[ I(\epsilon)=\int ^1_{\epsilon }\frac{dx}{\sqrt{x}}=2\sqrt{x}|^1_{\epsilon }=2(1-\sqrt{\epsilon })\rightarrow 2 \]

при $\epsilon \rightarrow +0$. Таким образом, исходный интеграл является сходящимся несобственным интегралом второго рода, причем он равен 2.

Рассмотрим вариант, когда разрыв второго рода подинтегральной функции имеется на верхнем пределе интервала интегрирования. Этот случай можно свести к предыдущему, сделав замену переменной $x=-t$ и затем переставив пределы интегрирования.

Рассмотрим вариант, когда разрыв второго рода у подинтегральной функции имеется внутри интервала интегрирования, в точке $c \in (a,\,b)$. В данном случае исходный интеграл

\begin{equation} I=\int _a^bf(x)\,dx (23) \label{intr3} \end{equation}

представляют в виде суммы

\[ I=I_1+I_2, \quad I_1=\int _a^cf(x)\,dx +\int _c^df(x)\,dx. \]

Определение. Если оба интеграла $I_1, \, I_2$ сходятся, то несобственный интеграл (23) называют сходящимся и ему приписывают значение, равное сумме интегралов $I_1, \, I_2$, функцию $f(x)$ называют интегрируемой на интервале $\left[ a, \, b\right]$. Если хотя бы один из интегралов $I_1,\, I_2$ является расходящимся, несобственный интеграл (23) называют расходящимся.

Сходящиеся несобственные интегралы 2 рода обладают всеми стандартными свойствами обычных определенных интегралов.

1. Если $f(x)$, $g(x)$ интегрируемы на интервале $\left[ a, \,b \right ]$, то их сумма $f(x)+g(x)$ также интегрируема на этом интервале, причем \[ \int _a^{b}\left(f(x)+g(x)\right)dx=\int _a^{b}f(x)dx+\int _a^{b}g(x)dx. \] 2. Если $f(x)$ интегрируема на интервале $\left[ a, \, b \right ]$, то для любой константы $C$ функция $C\cdot f(x)$ также интегрируема на этом интервале, причем \[ \int _a^{b}C\cdot f(x)dx=C \cdot \int _a^{b}f(x)dx. \] 3. Если $f(x)$ интегрируема на интервале $\left[ a, \, b \right ]$, причем на этом интервале $f(x)>0$, то \[ \int _a^{b} f(x)dx\,>\,0. \] 4. Если $f(x)$ интегрируема на интервале $\left[ a, \, b \right ]$, то для любого $c\in (a, \,b)$ интегралы \[ \int _a^{c} f(x)dx, \quad \int _c^{b} f(x)dx \] тоже сходятся, причем \[ \int _a^{b}f(x)dx=\int _a^{c} f(x)dx+\int _c^{b} f(x)dx \] (аддитивность интеграла по интервалу).

Рассмотрим интеграл

\begin{equation} I=\int _0^{1}\frac{1}{x^k}\,dx. (24) \label{mod2} \end{equation}

Если $k>0$, подинтегральная функция стремится к $\infty$ при $x \rightarrow +0$, так что интеграл - несобственный второго рода. Введем функцию

\[ I(\epsilon)=\int _{\epsilon}^{1}\frac{1}{x^k}\,dx. \]

В данном случае первообразная известна, так что

\[ I(\epsilon)=\int _{\epsilon}^{1}\frac{1}{x^k}\,dx\,=\frac{x^{1-k}}{1-k}|_{\epsilon}^1= \frac{1}{1-k}-\frac{\epsilon ^{1-k}}{1-k}. \]

при $k \neq 1$,

\[ I(\epsilon)=\int _{\epsilon}^{1}\frac{1}{x}\,dx\,=lnx|_{\epsilon}^1= -ln \epsilon. \]

при $k = 1$. Рассматривая поведение при $\epsilon \rightarrow +0$, приходим к выводу, что интеграл (20) сходится при $k

10.2.2 Признаки сходимости несобственных интегралов 2 рода

Теорема (первый признак сравнения). Пусть $f(x)$, $g(x)$ - непрерывны при $x\in (a,\,b)$, причем $0 1. Если интеграл \[ \int _a^{b}g(x)dx \] сходится, то сходится и интеграл \[ \int _a^{b}f(x)dx. \] 2. Если интеграл \[ \int _a^{b}f(x)dx \] расходится, то расходится и интеграл \[ \int _a^{b}g(x)dx. \]

Теорема (второй признак сравнения). Пусть $f(x)$, $g(x)$ - непрерывны и положительны при $x\in (a,\,b)$, причем существует конечный предел

\[ \theta = \lim_{x \rightarrow a+0} \frac{f(x)}{g(x)}, \quad \theta \neq 0, \, +\infty. \]

Тогда интегралы

\[ \int _a^{b}f(x)dx, \quad \int _a^{b}g(x)dx \]

сходятся или расходятся одновременно.

Рассмотрим интеграл

\[ I=\int _0^{1}\frac{1}{x+\sin x}\,dx. \]

Подинтегральное выражение - положительная функция на интервале интегрирования, подинтегральная функция стремится к $\infty$ при $x \rightarrow +0$, так что наш интеграл - несобственный второго рода. Далее, при $x \rightarrow +0$ имеем: если $g(x)=1/x$, то

\[ \lim _{x \rightarrow +0}\frac{f(x)}{g(x)}=\lim _{x \rightarrow +0}\frac{x}{x+\sin x}=\frac{1}{2} \neq 0,\, \infty \, . \]

Применяя второй признак сравнения, приходим к выводу, что наш интеграл сходится или расходится одновременно с интегралом

\[ \int _0^{+1}\frac{1}{x}\,dx . \]

Как было показано в предыдущем примере, этот интеграл расходится ($k=1$). Следовательно, исходный интеграл тоже расходится.

Вычислить несобственный интеграл или установить его сходимость (расходимость).

1. \[ \int _{0}^{1}\frac{dx}{x^3-5x^2}\,. \] 2. \[ \int _{3}^{7}\frac{x\,dx}{(x-5)^2}\,. \] 3. \[ \int _{0}^{1}\frac{x\,dx}{\sqrt{1-x^2}}\,. \] 4. \[ \int _{0}^{1}\frac{x^3\,dx}{1-x^5}\,. \] 5. \[ \int _{-3}^{2}\frac{dx}{(x+3)^2}\,. \] 6. \[ \int _{1}^{2}\frac{x^2\,dx}{(x-1)\sqrt{x-1}}\,. \] 7. \[ \int _{0}^{1}\frac{dx}{\sqrt{x+x^2}}\,. \] 8. \[ \int _{0}^{1/4}\frac{dx}{\sqrt{x-x^2}}\,. \] 9. \[ \int _{1}^{2}\frac{dx}{xlnx}\,. \] 10. \[ \int _{1}^{2}\frac{x^3\,dx}{\sqrt{4-x^2}}\,. \] 11. \[ \int _{0}^{\pi /4}\frac{dx}{\sin ^4x}\,. \]

Тема НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

В теме «Определенный интеграл» было рассмотрено понятие определенного интеграла для случая конечного промежутка
и ограниченной функции
(см. теорему 1 из §3). Теперь займемся обобщением этого понятия для случаев бесконечного промежутка и неограниченной функции. Необходимость такого обобщения показывают, например, такие ситуации.

1. Если, используя формулу для длины дуги, попытаться вычислить длину четверти окружности
,
, то придем к интегралу от неограниченной функции:

, где
.

2. Пусть тело массой
движется по инерции в среде с силой сопротивления
, где
- скорость тела. Используя второй закон Ньютона (
, где
ускорение), получим уравнение:
, где
. Нетрудно показать, что решением этого (дифференциального!) уравнения является функция
Если нам потребуется вычислить путь, пройденный телом до полной остановки, т.е. до момента, когда
, то придем к интегралу по бесконечному промежутку:

§1. Несобственные интегралы 1-го рода

I Определение

Пусть функция
определена и непрерывна на промежутке
. Тогда для любого
она интегрируема на промежутке
, то есть существует интеграл
.

Определение 1 . Конечный или бесконечный предел этого интеграла при
называют несобственным интегралом 1-го рода от функции
по промежутку
и обозначают символом
. При этом, если указанный предел конечен, то несобственный интеграл называют сходящимся, в противном случае (
или не существует) – расходящимся.

Итак, по определению

Примеры

2.
.

3.
– не существует.

Несобственный интеграл из примера 1 сходится, в примерах 2 и 3 интегралы расходятся.

II Формула Ньютона – Лейбница для несобственного интеграла первого рода

Пусть
- некоторая первообразная для функции
(сущест-вует на
, т.к.
- непрерывна). Тогда

Отсюда ясно, что сходимость несобственного интеграла (1) равносильна существованию конечного предела
. Если этот предел обозначить
, то можно написать для интеграла (1) формулу Ньютона-Лейбница:

, где
.

Примеры .

5.
.

6. Более сложный пример:
. Сначала найдем первообразную:

Теперь можем найти интеграл , учитывая, что

:

III Свойства

Приведем ряд свойств несобственного интеграла (1), которые вытекают из общих свойств пределов и определенного интеграла:

IV Другие определения

Определение 2 . Если
непрерывна на
, то

.

Определение 3 . Если
непрерывна на
, то принимают по определению

(– произвольное),

причем несобственный интеграл в левой части сходится, если только оба ин-теграла в правой части сходятся.

Для этих интегралов, как и для интеграла (1) можно написать соответствующие формулы Ньютона – Лейбница.

Пример 7 .

§2. Признаки сходимости несобственного интеграла 1-го рода

Чаще всего несобственный интеграл вычислить по определению не-возможно, поэтому используют приближенное равенство

(для больших ).

Однако, это соотношение имеет смысл лишь для сходящихся интегралов. Необходимо иметь методы выяснения поведения интеграла минуя определение.

I Интегралы от положительных функций

Пусть
на
. Тогда определенный интеграл
как функция верхнего предела есть функция возрастаю-щая (это следует из общих свойств определенного интеграла).

Теорема 1 . Несобственный интеграл 1 го рода от неотрицательной функ-ции сходится тогда и только тогда, когда функция
остается ограниченной при увеличении.

Эта теорема – следствие общих свойств монотонных функций. Практического смысла теорема почти не имеет, но позволяет получить т.н. признаки сходимости.

Теорема 2 (1-й признак сравнения). Пусть функции
и
непре-рывны на
и удовлетворяют неравенству
. Тогда:

1) если интеграл
сходится, то и
сходится;

2) если интеграл
расходится, то и
расходится.

Доказательство . Обозначим:
и
. Так как
, то

. Пусть интеграл
сходится, тогда (в силу теоремы 1) функция
‒ ограничена. Но тогда и
ограничена, а значит, интеграл
тоже сходится. Аналогично доказывается и вторая часть теоремы.

Этот признак не применим в случае расходимости интеграла от
или сходимости интеграла от
. Этот недостаток отсутствует у 2-го признака сравнения.

Теорема 3 (2-й признак сравнения). Пусть функции
и
непрерывны и неотрицательны на
. Тогда, если
при
, то несобственные интегралы
и
сходятся или расходятся одновременно.

Доказательство . Из условия теоремы получим такую цепочку равно-сильных утверждений:

, ,

.

Пусть, например,
. Тогда:

Применим теорему 2 и свойство 1) из §1 и получим утверждение теоремы 3.

В качестве эталонной функции, с которой сравнивают данную, высту-пает степенная функция
,
. Предлагаем студентам самим доказать, что интеграл

сходится при
и расходится при
.

Примеры . 1.
.

Рассмотрим подынтегральную функцию на промежутке
:

,
.

Интеграл
сходится, ибо
. По 2-му признаку сравнения сходится и интеграл
, а в силу свойства 2) из §1 сходится и исход-ный интеграл.

2.
.

Так как
, тоcуществует
такое, что при

. Для таких значений переменной:

Известно, что логарифмическая функция растет медленнее степенной, т.е.

,

а значит, начиная с некоторого значения переменной, эта дробь меньше 1. Поэтому

.

Интеграл сходится как эталонный. В силу 1-го признака сравнения сходится и
. Применяя 2-й признак, получим, что и интеграл
сходится. И снова свойство 2) из §1 доказывает сходимость исходного интеграла.

Несобственные интегралы первого рода. По сути это тот же определённый интеграл, но в случаях, когда интегралы имеют бесконечный верхний или нижний пределы интегрирования, или оба предела интегрирования бесконечны.

Несобственные интегралы второго рода. По сути это тот же определённый интеграл, но в случаях, когда интеграл берётся от неограниченных функций, подынтегральная функция в конечном числе точек конечного отрезка интегрирования не имеет, обращаясь в бесконечность.

Для сравнения. При введении понятия определённого интеграла предполагалось, что функция f (x ) непрерывна на отрезке [a , b ], а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью. Некоторые задачи приводят к необходимости отказаться от этих ограничений. Так появляются несобственные интегралы.

Геометрический смысл несобственного интеграла выясняется довольно просто. В случае, когда график функции y = f (x ) находится выше оси Ox , определённый интеграл выражает площадь криволинейной трапеции, ограниченной кривой y = f (x ) , осью абсцисс и ординатами x = a , x = b . В свою очередь несобственный интеграл выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями y = f (x ) (на рисунке ниже - красного цвета), x = a и осью абсцисс.

Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:

Площадь бесконечной криволинейной трапеции может быть конечным числом и в этом случае несобственный интеграл называется сходящимся. Площадь может быть и бесконечностью и в этом случае несобственный интеграл называется расходящимся.

Использование предела интеграла вместо самого несобственного интеграла. Для того, чтобы вычислить несобственный интеграл, нужно использовать предел определённого интеграла. Если этот предел существует и конечен (не равен бесконечности), то несобственный интеграл называется сходящимся, а в противном случае - расходящимся. К чему стремится переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода или второго рода. Узнаем об этом сейчас же.

Несобственные интегралы первого рода - с бесконечными пределами и их сходимость

Несобственные интегралы с бесконечным верхним пределом

Итак, запись несобственного интеграла как отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен.

Определение. Несобственным интегралом с бесконечным верхним пределом интегрирования от непрерывной функции f (x ) на промежутке от a до ∞ называется предел интеграла этой функции с верхним пределом интегрирования b и нижним пределом интегрирования a при условии, что верхний предел интегрирования неограниченно растёт , т.е.

.

Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся , а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся и ему не приписывается никакого значения.

Пример 1. Вычислить несобственный интеграл (если он сходится).

Решение. На основании определения несобственного интеграла находим

Так как предел существует и равен 1, то и данный несобственный интеграл сходится и равен 1.

В следующем примере подынтегральная функция почти как в примере 1, только степень икса - не двойка, а буква альфа, а задача состоит в исследовании несобственного интеграла на сходимость. То есть предстоит ответить на вопрос: при каких значениях альфы данный несобственный интеграл сходится, а при каких расходится?

Пример 2. Исследовать на сходимость несобственный интеграл (нижний предел интегрирования больше нуля).

Решение. Предположим сначала, что , тогда

В полученном выражении перейдём к пределу при :

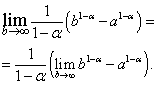
Нетрудно видеть, что предел в правой части существует и равен нулю, когда , то есть , и не существует, когда , то есть .

В первом случае, то есть при имеет место . Если , то и не существует.

Вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходится при .

Применяя к изучаемому виду несобственного интеграла формулу Ньютона-Лейбница , можно вывести следующую очень похожую на неё формулу:

.

Это обобщённая формула Ньютона-Лейбница.

Пример 3. Вычислить несобственный интеграл (если он сходится).

Предел этого интеграла существует:

Второй интеграл, составляющий сумму, выражающую исходный интеграл:

Предел этого интеграла также существует:

.

Находим сумму двух интегралов, являющуюся и значением исходного несобственного интеграла с двумя бесконечными пределами:

Несобственные интегралы второго рода - от неограниченных функций и их сходимость

Пусть функция f (x ) задана на отрезке от a до b и неограниченна на нём. Предположим, что функция обращается в бесконечность в точке b , в то время как во всех остальных точках отрезка она непрерывна.

Определение. Несобственным интегралом функции f (x ) на отрезке от a до b называется предел интеграла этой функции с верхним пределом интегрирования c , если при стремлении c к b функция неограниченно возрастает, а в точке x = b функция не определена , т.е.

.

Если этот предел существует, то несобственный интеграл второго рода называется сходящимся, в противном случае - расходящимся.

Используя формулу Ньютона-Лейбница, выводим.

1.Определение несобственного интеграла второго рода

Пусть f (x ) задана на [a ;b ], но неограниченна на нём. Пусть для определённости f (x ) неограниченна в левой окрестности точки b : , но в любом промежутке функция интегрируема. В этом случае точку b называют особой точкой.

Определение. Несобственным интегралом второго рода функции f (x ) на [a ;b ] называется конечный или бесконечный предел интеграла при

Если предел (1) существует и конечен, то говорят, что интеграл сходится, и значение предела считают значением интеграла. Если предел (1) не существует или равен бесконечности, то говорят, что интеграл расходится.

Аналогично определяется интеграл функции f (x ), неограниченной в правой окрестности точки а :

Пример 1. Исследовать на сходимость .

D 1) : интеграл расходится.

Итак, интеграл сходится при , расходится при . D

2. Формула Ньютона-Лейбница для несобственного интеграла второго рода

Пусть функция f (x ) определена и непрерывна в интервале [a ;b ) и вблизи точки b функция неограниченна (b - особая точка функции f (x )). Тогда для f (x ) в этом промежутке существует первообразная F (x ) и "h >0 по формуле Ньютона-Лейбница имеем

Отсюда следует, что несобственный интеграл (1) существует тогда и только тогда, когда существует конечный предел . В этом случае функция F (x ) является непрерывной на отрезке [a ;b ]. Тогда, переходя в (2) к пределу при h ®0, получим формулу Ньютона-Лейбница для несобственного интеграла второго рода

Итак , для вычисления несобственных интегралов второго рода можно использовать формулу Ньютона-Лейбница, если функция F (x ) непрерывна на отрезке [a ;b ] и F¢ (x )=f (x ) во всех точках, где f (x ) конечна.

Пример 2. Вычислить .

D х =0 – особая точка. Первообразная непрерывна на [-1;27], в том числе, и в точке х =0, следовательно, можно применить формулу Ньютона-Лейбница:

Пример 3. Исследовать на сходимость .

D х =0 – особая точка. Первообразная имеет в точке х =0 бесконечный разрыв. Следовательно, данный интеграл расходится и равен ¥.

Заметим , что если не обратить на это внимание и формально применить формулу Ньютона-Лейбница, то получим неверный результат:

3. Несобственные интегралы второго рода от неотрицательных функций

Теорема 1. Пусть f (x )³0 на [a ;b ) и интегрируема на [a ;b-h ] "h >0. Для сходимости несобственного интеграла (1) необходимо и достаточно, чтобы множество интегралов (h >0) ограничено сверху. В противном случае интеграл (1) расходится и равен ¥.

Для несобственных интегралов второго рода, как и для несобственных интегралов первого рода, имеют место теоремы сравнения 2 и 3. Сформулируем их без доказательства.

Теорема 2. Пусть функции f и g неотрицательны на [a ;b ) и интегрируемы на [a ;b-h ] "h >0. Пусть на [a ;b ) выполнено

Тогда: 1) из сходимости интеграла следует сходимость интеграла ;

2) из расходимости интеграла следует расходимость интеграла .

Теорема 3. Пусть функции f и g неотрицательны на [a ;b ) и интегрируемы на [a ;b-h ] "h >0. Если существует (0£k £¥), то

1) из сходимости интеграла при k <¥ следует сходимость интеграла ,

2) из расходимости интеграла при k >0 следует расходимость интеграла .

Замечание. Если в условиях теоремы 3 0<k< ¥ (конечное число, не равное 0), то интегралы и сходятся или расходятся одновременно.

В качестве функций сравнения удобно брать степенные функции: для промежутка [a ;b ) , а для промежутка (a ;b ] . Соответствующие интегралы , сходятся при , расходится при (в этом легко убедиться, сведя указанные интегралы линейной заменой переменной к интегралу , рассмотренному в примере 1).

Пример 4. Исследовать на сходимость . .

Сходится . Значит, по теореме 3, сходится и . D

Пример 6. Исследовать на сходимость .

D х =0 – особая точка функции f (x )=lnx . Пусть .

Это имеет место , в том числе, и при a <1, когда сходится. Значит, по теореме 3 сходится и данный интеграл. D